Projet d'Ouverture à la recherche : Machine Learning pour la coloration de graphes

Sujet

Le problème de coloration de graphe est un problème dit NP-difficile, c’est-à-dire que c’est un problème pour lequel il n'existe pas d'algorithme efficace connu pour le résoudre de manière déterministe en un temps raisonnable. Un algorithme déterministe est un algorithme qui, pour une entrée donnée, produira toujours la même sortie indépendamment de la personne qui l'exécute et du moment de son exécution.

Le problème de coloration de graphe est le fait d’attribuer une couleur à chaque nœud d'un graphe de telle sorte que deux sommets adjacents n’ont jamais la même couleur. Il existe différents types de coloration de graphe. Lors de notre projet nous nous sommes intéressées à la coloration minimale dans un graphe et à la coloration de Grundy.

La coloration minimale implique que le nombre de couleurs utilisées soit minimal, par conséquent il s’agit du plus petit nombre de couleurs possibles pour la coloration d’un graphe.

La coloration de Grundy, quant à elle, suppose que l'on doit colorer un graphe avec un maximum de couleurs de telle sorte que quand on colore un sommet de la couleur k, celui-ci doit être adjacent à un sommet de chaque couleur inférieure à k.

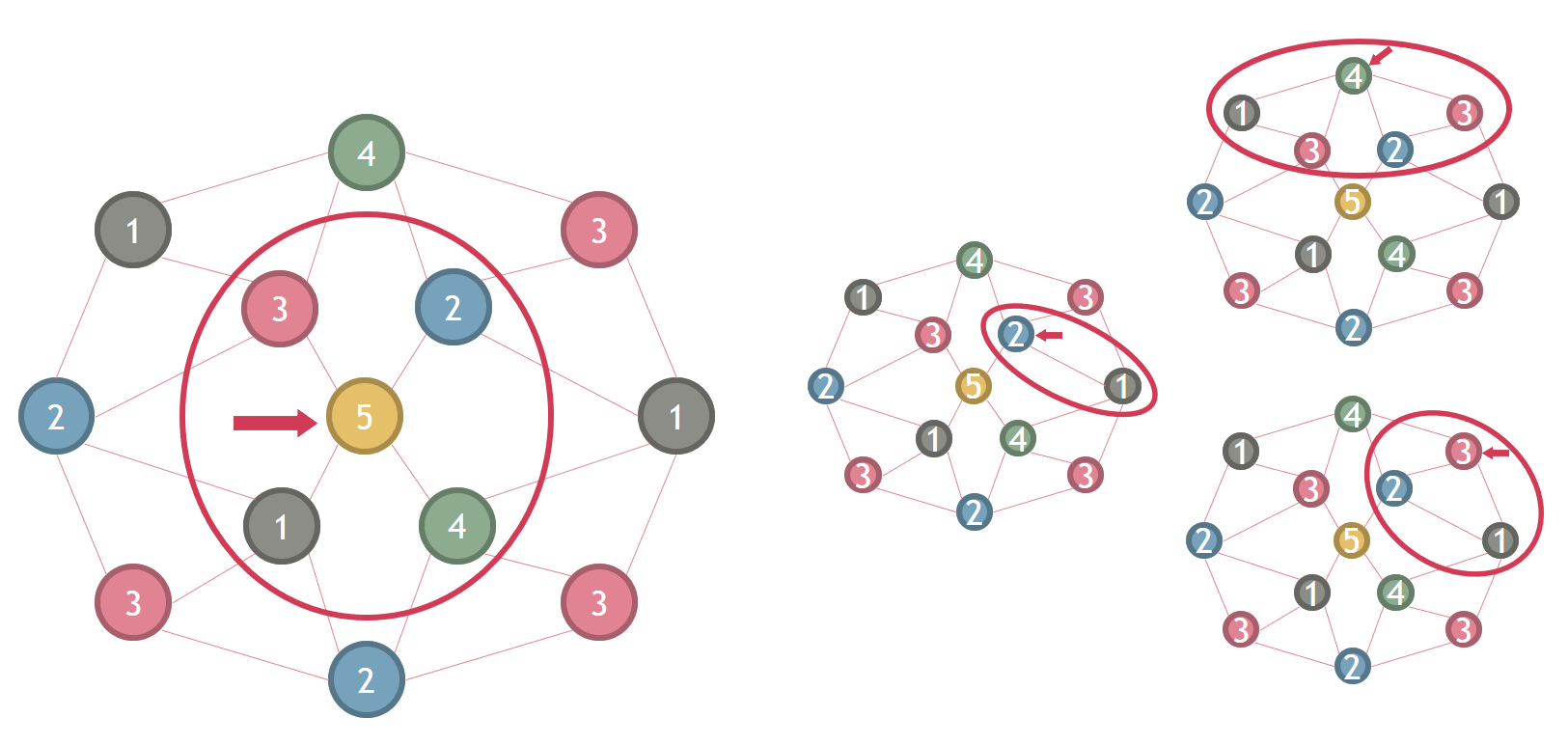
Par exemple, sur le graphe ci-dessous, le sommet coloré 5 est bien adjacent à un sommet coloré 4, un sommet coloré 3, un sommet coloré 2 et un sommet coloré 1.

Implémentation

Q-Learning

J'ai, en particulier, implémenté un algorithme de Q-learning. Le Q-learning fait partie des algorithmes d'apprentissage par renforcement. Il est basé sur un système de récompenses, sur des états et sur des actions. Dans cet algorithme, un agent reçoit une récompense s’il s’approche du but en effectuant une action.

Les états représentent les différents nœuds du graphe et les actions les différentes couleurs que peuvent prendre les nœuds du graphe. La fonction de Q-Learning prend en paramètre :

• G : un graphe
• episodes : le nombre d’épisodes (itérations) à lancer
• α : le learning rate (taux d’apprentissage). Le learning rate détermine la taille des pas que le modèle prend lors de l'optimisation de ses paramètres en fonction de l'erreur de prédiction. Si le learning rate est trop petit, le modèle peut prendre beaucoup de temps à converger vers une solution optimale, tandis qu'un learning rate trop élevé peut entraîner une convergence rapide, mais instable ou imprécise. Ainsi, le choix du bon learning rate est crucial pour obtenir un modèle efficace et précis.
• γ : le discount factor (facteur de réduction). C’est un nombre compris entre 0 et 1 qui détermine le degré de remise des récompenses futures. Un gamma proche de 0 signifie que le modèle ne se soucie que des récompenses immédiates et ignore les récompenses futures, tandis qu'un gamma proche de 1 signifie que le modèle prend en compte les récompenses futures autant que les récompenses immédiates.
• ε : l’exploration rate (taux d’exploration). Le taux d'exploration permet d’équilibrer l'exploration et l'exploitation des actions. Il détermine la probabilité de choisir une action au hasard plutôt que l'action optimale.

Cet algorithme utilise une Q-table permettant de stocker pour chaque paire état/action sa Q-value. La Q-Value est au départ de 0 mais à chaque itération, et pour chaque nœud parcouru, elle est mise à jour. Pour cela, l’algorithme prend en compte les valeurs des itérations précédentes afin de maximiser la Q-value et de trouver la couleur optimale pour chaque nœud.

La formule suivante permet de mettre à jour la Q-value pour chaque épisode et pour chaque nœud exploré lors de cet épisode.

Q[s][a] = Q[s][a] + α * (reward + γ * max(Q[next_node]) - Q[s][a])

Avec s l’état (state) courant et a l’action (couleur) choisie. La récompense varie en fonction de la coloration choisie. À la fin de l’algorithme les valeurs convergent et nous pouvons afficher le graphe ainsi coloré. Voici le pseudo-code de l'algorithme de Q-Learning :

Coloration minimale

Dans le cas de la coloration minimale, la fonction colorize permet facilement de déterminer la couleur à choisir.

Si un nombre tiré aléatoirement entre 0 et 1 est inférieur à l’exploration rate ε, alors nous choisissons une couleur aléatoire sous condition qu’elle ne soit pas déjà choisie par un des voisins du nœud.

Si ce nombre est supérieur à l’exploration rate, nous essayons d’optimiser la valeur choisie, c’est-à-dire de prendre la Q-Value la plus élevée dans notre Q-table. Une fois cette valeur obtenue, nous pouvons récupérer l’action (couleur) correspondante.

Comme précédemment, nous vérifions que cette valeur n’est pas la couleur d’un des voisins du nœud. Une fois cette vérification effectuée, si le nœud suivant n’est pas voisin d’un nœud actuel alors nous renvoyons l’action trouvée. Si les deux nœuds sont voisins, nous comparons la Q-Value obtenue avec la Q-Value maximale du nœud suivant. Si les deux valeurs correspondent à la même action (même couleur), mais que la valeur du nœud suivant est supérieure, il est alors plus intéressant de choisir cette couleur pour le nœud suivant. En effet, deux nœuds ne peuvent pas avoir la même couleur et notre but et de maximiser les Q-Values. Dans ce cas-là, le nœud prendra comme couleur sa deuxième plus grande Q-Value dont la couleur ne correspond pas à la couleur d’un de ses voisins.

Une fois la couleur déterminée, nous pouvons déterminer la récompense associée. Si cette couleur n’appartenait pas encore au tableau de couleur de cet épisode, alors la récompense est de -1, sinon elle est de 1.

Voici le pseudo-code correspondant à cette fonction :