Interaction Multi-Agents : Taquin

Sujet

On souhaite développer un système multi-agent dont le rôle est de reconstruire un Puzzle selon l’approche cognitive. Dans la modélisation qu’on vous propose, chaque agent représente une case de ce Puzzle dont la taille est de n*n. Pour simplifier, dans la première étape, nous retiendrons n=5. Chaque case est numérotée, de 1 à n*n, et occupe un emplacement dans ce Puzzle (cf. Fig1.). Par exemple la case numéro 4, représentée ci-dessous par une étoile de couleur grisée (ligne 1 colonne 4), doit normalement se retrouver en fin de jeu à la position (1, 2), si on veut que le Puzzle soit correctement reconstitué. Initialement, cette case peut être à n’importe quelle position, par exemple (1,4), comme le montre la figure ci-dessous.

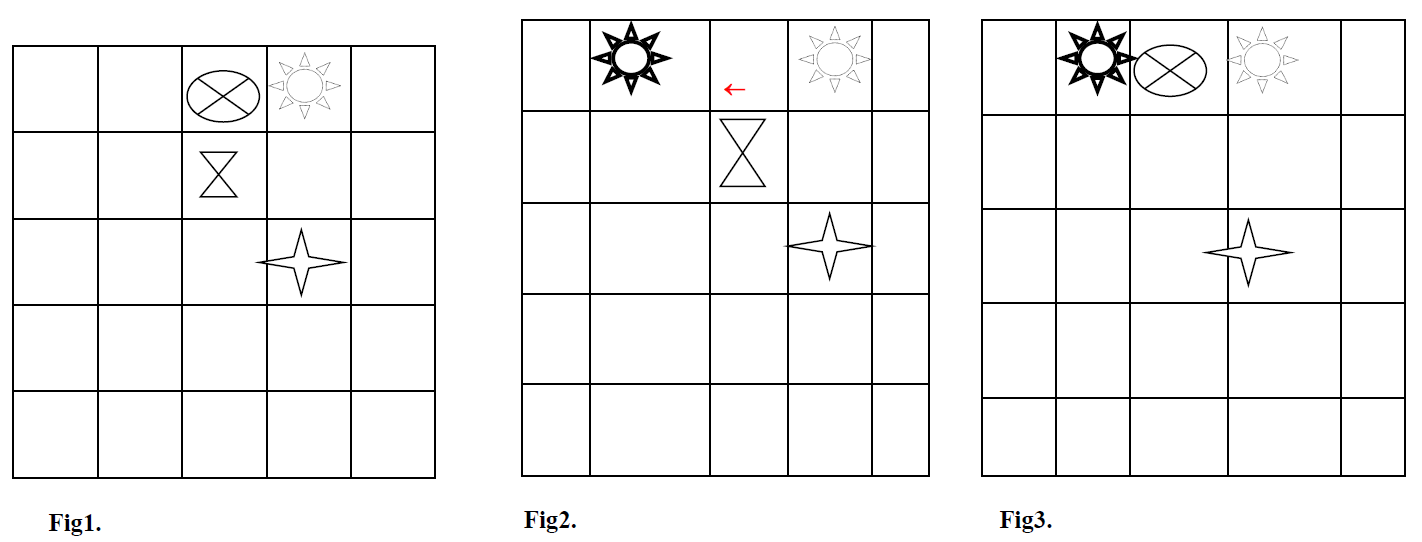
Pour déplacer ces cases, chaque agent peut effectuer des sauts. Par exemple, pour aller de la position (1, 4) à la position (1, 2) plusieurs déplacements pour la case « étoile » sont possibles selon l’occupation ou pas de ses cases adjacentes. Les deux figures suivantes (2 et 3) décrivent deux déplacements possibles de cette case. Sur la figure 2, la case étoile se déplace directement de droite à gauche pour atteindre sa position finale puisqu’aucune case ne se trouve devant celle-ci. La figure 3 décrit une autre situation dans laquelle la case étoile est obligée de contourner la case « croix-encerclée » qui se trouve sur son chemin en passant par la case (2,4) et ce pour rejoindre sa position finale.

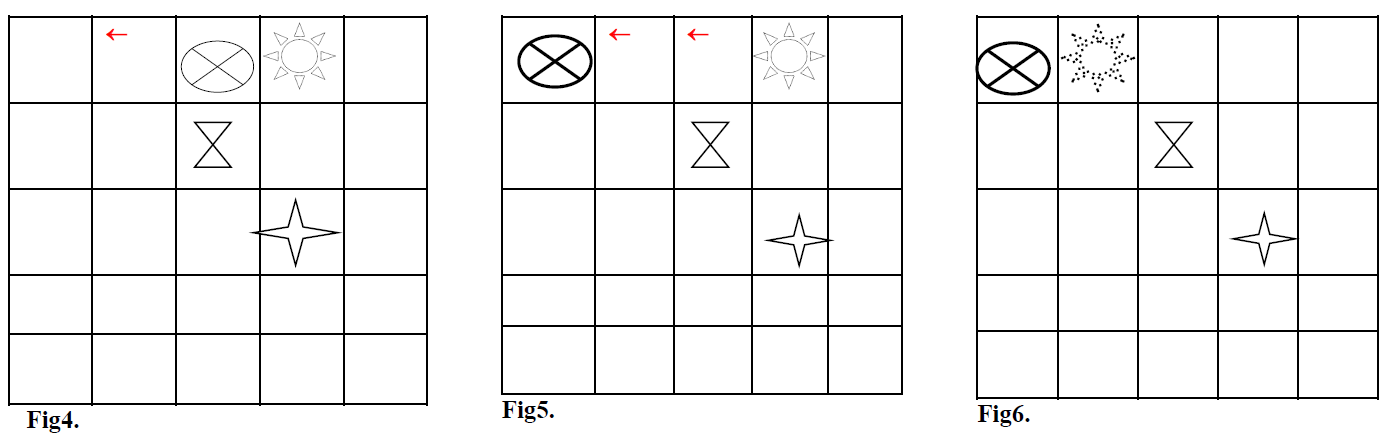
Il s’agit, dans un premier temps, de modéliser ce système par l’approche multi-agent.
1. Nous commencerons par définir, dans un premier temps, des stratégies simples dans lesquelles les agents effectuent des déplacements uniquement sur la base de leur perception de l’occupation des cases voisines ou pas. Par exemple :
1.1. Un agent choisit directement de se déplacer si le chemin vers sa case est libre.
1.2. Il se déplace uniquement après avoir identifié le meilleur chemin à emprunter vers sa case.
2. Dans une approche purement cognitive, des stratégies plus sophistiquées consisteraient pour un agent à choisir d’interagir avec ses voisins avant de se déplacer. L’agent demande d’abord à son voisin de lui libérer la case voisine avant de se déplacer lui-même. Il consiste en cela à envoyer un message à son voisin qui une fois son accord et son déplacement effectués l’agent entamera son déplacement. Les trois figures suivantes (4, 5 et 6) illustrent cette succession de déplacements de pour la case « croix-encerclée » pour permettre à la case « étoile » de rejoindre sa position.

Réalisation

Notre taquin est représenté par une grille de taille n*n. Nous pouvons modifier la taille (n) souhaitée dans le main, mais également modifier le nombre de pièces que nous voulons placer dans la grille. Évidemment, si le nombre de pièces indiqué n’appartient pas à l’intervalle [1, (n*n)-1], nous mettons automatiquement le plus grand nombre de pièces possibles, c’est-à-dire (n*n)-1 afin de ne laisser qu’un seul emplacement vide dans la grille.

Les agents du système, représentés chacun par une case du taquin peuvent se déplacer. Chaque case a pour symbole un numéro unique qui représente la position de sa destination sur la grille (la case numéro 1 se trouve en haut à gauche et la case de numéro maximal se trouve en bas à droite). Cela permet de se rendre compte rapidement de la position d’un agent par rapport à sa destination. Afin de trouver le plus court chemin pour qu’un agent atteigne sa destination, nous avons implémenté l’algorithme A*.

Nous avons ensuite développé un système d’échanges de messages entre les différents agents lorsque le chemin défini par A* est bloqué. Ce système de messages permet de demander à l’agent qui bloque le passage de se déplacer pour libérer l’accès. Chaque message est composé d’un auteur, d’une instruction simple et d’un contenu. Nous avons implémenté un unique type de message : la demande de déplacement (“move”). Tout agent va régulièrement consulter sa boîte de messagerie et déterminer s’il répond ou non aux différentes demandes.